Queuing Theory
Queuing theory deals with problems which involve queuing (or waiting).
Queueing theory is the mathematical study of waiting lines or queues.
The theory enables mathematical analysis of several related processes, including arriving at the (back of the) queue, waiting in the queue (essentially a storage process), and being served by the server(s) at the front of the queue.
The theory permits the derivation and calculation of several performance measures including the average waiting time in the queue or the system, the expected number waiting or receiving service and the probability of encountering the system in certain states, such as empty, full, having an available server or having to wait a certain time to be served.
Typical examples might be:
Queueing theory is the mathematical study of waiting lines or queues.
The theory enables mathematical analysis of several related processes, including arriving at the (back of the) queue, waiting in the queue (essentially a storage process), and being served by the server(s) at the front of the queue.
The theory permits the derivation and calculation of several performance measures including the average waiting time in the queue or the system, the expected number waiting or receiving service and the probability of encountering the system in certain states, such as empty, full, having an available server or having to wait a certain time to be served.
Typical examples might be:
banks/supermarkets - waiting for service
computers - waiting for a response
failure situations - waiting for a failure to occur e.g. in a piece of machinery
public transport - waiting for a train or a bus
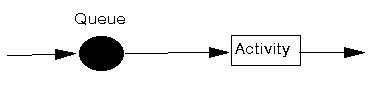
Typically we can talk of this individual sub-system as dealing with customers queuing for service. To analyse this sub-system we need information relating to :
Arrival process
how customers arrive e.g. singly or in groups (batch or bulk arrivals)
how the arrivals are distributed in time (e.g. what is the probability distribution of time between successive arrivals (the interarrival time distribution))
Service mechanism:
A description of the resources needed for service to begin
How long the service will take - the service time distribution.
Queue characteristics:
How, from the set of customers waiting for service, do we choose the one to be served next (e.g. FIFO (first-in first-out) - also known as FCFS (first-come first served); LIFO (last-in first-out); randomly) (this is often called the queue discipline)
do we have:
Balking (customers deciding not to join the queue if it is too long)
Reneging (customers leave the queue if they have waited too long for service)
Jockeying (customers switch between queues if they think they will get served faster by so doing)
A queue of finite capacity or (effectively) of infinite capacity
computers - waiting for a response
failure situations - waiting for a failure to occur e.g. in a piece of machinery
public transport - waiting for a train or a bus
In designing queueing systems we need to aim for a balance between service to customers (short queues implying many servers) and economic considerations (not too many servers).
In essence all queuing systems can be broken down into individual sub-systems consisting of entities queuing for some activity as shown below.
Typically we can talk of this individual sub-system as dealing with customers queuing for service. To analyse this sub-system we need information relating to :
Arrival process
how customers arrive e.g. singly or in groups (batch or bulk arrivals)
how the arrivals are distributed in time (e.g. what is the probability distribution of time between successive arrivals (the interarrival time distribution))
Service mechanism:
A description of the resources needed for service to begin
How long the service will take - the service time distribution.
Queue characteristics:
How, from the set of customers waiting for service, do we choose the one to be served next (e.g. FIFO (first-in first-out) - also known as FCFS (first-come first served); LIFO (last-in first-out); randomly) (this is often called the queue discipline)
do we have:
Balking (customers deciding not to join the queue if it is too long)
Reneging (customers leave the queue if they have waited too long for service)
Jockeying (customers switch between queues if they think they will get served faster by so doing)
A queue of finite capacity or (effectively) of infinite capacity
