*من المهارات التي يحتاجها المديرون والمهندسون الصناعيون والكثير من الناس مهارة تحديد العلاقة بين متغيرين أو أكثر. هل هناك علاقة بين حجم المبيعات في كل منطقة وأسلوب التسويق المتبع؟ هل هناك علاقة بين عدد المشاكل في المعدات ودرجة حرارة الجو؟ هل هناك علاقة بين مرض كذا وجودة مياه الشرب؟ هل هناك علاقة بين رضا الموظفين عن عملهم وجودة الوجبة التي تقدم لهم؟ هذه النوعية من الأسئلة نتعرض لها كثيرا في العمل ونحاول البحث عن إجابة مبنية على أساس صحيح. في هذه المقالة والمقالات التالية -إن شاء الله- أحاول استعراض الادوات البسيطة التي تمكننا من الإجابة على مثل هذه الأسئلة.
1- الرسم البياني Scatter Diagram:
يمكننا أن رنسم العلاقة بين قيم المتغيرين لنرى إن كان الرسم يشير لوجود علاقة أم أنه يبين عدم وجود أي علاقة بين المتغيرين. يسمى هذا المنحنى بـ Scatter Plot أو Scatter Diagram وقد وجدت له عدة ترجمات باللغة العربية مثل: رسم بياني تنقيطي، رسم (شكل) الانتشار، رسم بياني مبعثر ورسم (مخطط) التشتت. الرسومات الآتية توضح امثلة للعلاقة بين متغيرين.
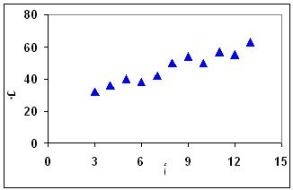
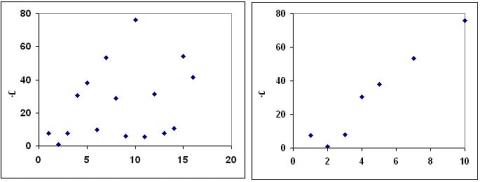
علاقة طردية (إيجابية)
هذا الرسم يظهر أن هناك علاقة طردية بين المتغير ب والمتغير أ فكلما ازداد أ ازداد ب. وإن كنا لا نستطيع التوصيل بخط مستقيم واحد بين كل النقاط ولكننا بمجرد النظر ندرك ان كل النقاط لها اتجاه واحد هو اتجاه العلاقة الطردية.
علاقة عكسية (سلبية)
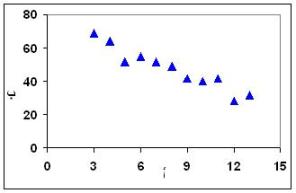
هذا الرسم يظهر علاقة عكسية فعندما كان أ يساوي 3 كان ب يساوي حوالي 70 وعندما زاد أ إلى 9 كان ب حوالي 40 وعندما ازداد أ إلى 12 كان ب حوالي 30. فكلما ازداد أ قل ب.
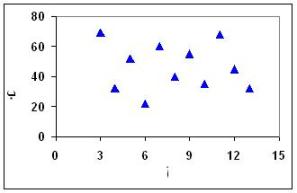
لا علاقة
هذا الرسم يوضح انه لا توجد أي علاقة بين تغير أ وتغير ب.
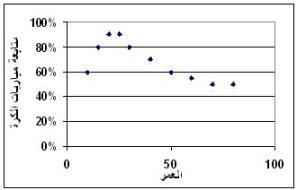
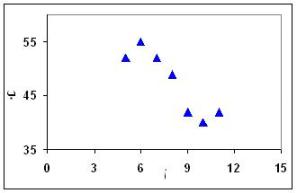
علاقة غير خطية
قد يظهر الرسم علاقة غير خطية وهذا من مميزات هذا الرسم. العلاقة الخطية هي العلاقة التي يمكن التعبير عنها بخط مستقيم مثل العلاقة الطردية أو العكسية السابق بيانهما. أما العلاقة غير الخطية فإنها تأخذ شكل منحنى. فمثلا قي الرسم أدناه نلاحظ العلاقة بين العمر ونسبة متابعة مباريات كرة القدم (هذه بيانات افتراضية). فهذا الرسم يوضح علاقة غير خطية ويمكن تحليلها وفهمها فمتابعة المباريات تزداد مع زيادة العمر ما بين 10 و20 عاما ثم تقل تدريجيا بداية من عمر 30 عاما. ويمكن فهم ذلك بأن الأطفال والشباب يبدؤون في حب الكرة تدريجيا فبعضهم لا يفهمها حتى سن الخامسة عشرة. والرجال من سن 30 سنة يبدؤون في الانشغال في أعمالهم فتقل نسبة متابعتهم للمباريات تدريجيا.
لاحظ أن تحليل هذه العلاقات لابد أن ينبع من دراسة وتحليل منطقي يعتمد على فهم الموضوع وتجميع بيانات داعمة لهذا التحليل.
علاقة وليس سببية:
إن وجدت علاقة طردية أو عكسية عن طريق الرسم البياني أو أي وسيلة أخرى فلا يمكنك أن تدعي أن أ هو سبب ب بل كل ما تستطيع قوله أن هناك علاقة بين المتغيرين. قد يكون أ وب يزيدان بسبب متغير آخر والذي هو سبب أ وب. فمثلا عند ارتفاع درجة حرارة الجو فإن درجة حرارة أي غرقة بالمنزل سترتفع وإن كانت بعض الغرف قد تكون درجة حرارتها مختلفة عن الأخرى حسب وضع الغرف من ناحية مواجهة الشمس والتهوية. فلو درسنا العلاقة بين درجة حرارة غرفة النوم ودرجة حرارة غرفة المعيشة فإن سنجد علاقة طردية واضحة. وهذا أمر طبيعي ولكن لا نستطيع أن نقول أن درجة حرارة غرفة النوم ترتفع نتيجة لارتفاع درجة حرارة غرفة المعيشة ولكن الحقيقة أن كلاهما يزيد كنتيجة لارتفاع درجة حرارة الجو الخارجي.
لا تنس أبدا أن كل وسائل تحديد العلاقة بين متغيرين أو أكثر هي وسائل لتحديد وجود علاقة وليس لتحديد وجود سببية.
الأمانة في عرض البيانات:
لابد من أن تكون أمينا في عرض البيانات فمثلا:
- لا تحاول تغيير مقياس الرسم لتظهر علاقة غير حقيقية أو تخفي علاقة حقيقية. فعندما تقوم بتكبير مقياس الرسم فقد لا يستطيع القارئ رؤية أي علاقة. وبالعكس فإن علاقة غير حقيقية يمكن أن تخدع القارئ بها إذا قمت بالتركيز على جزء صغير من المحور الرأسي.
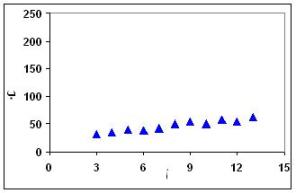
الرسم التالي هو لنفس العلاقة الطردية المذكورة في المثال السابق ولكن بعد تكبير محور ب لكي يغطي من صفر إلى 250. إنك لا تكاد ترى العلاقة الطردية الآن.
والرسم التالي هو لنفس العلاقة العكسية الواضحة المعروضة في المثال أعلاه ولكن بتحديد المحور ب بين 25 و 60 فقط. من الصعب تحديد علاقة من هذا الرسم.
- لا تحاول إخفاء بعض البيانات لكي تقنع القارئ بما تريد. عليك ان تعرض البيانات كما هي. لا تنتقِ النقاط التي تظهر علاقة ما او تخفي علاقة ما ولكن اعرض كل البيانات بأمانة.
الرسم التالي -على اليسار- يوضح العلاقة الحقيقية بين متغيرين حيث لا توجد أي علاقة. بينما الرسم على اليمين يظهر علاقة طردية قوية وذلك بعد تحديد المحور الأفقي بحد أقصى عشرة وكذلك إخفاء بعض النقاط.
- بالطبع لا تغير البيانات بل اعرضها كما هي فلا تغير أي رقم لكي يبدو الشكل كما تتمنى.
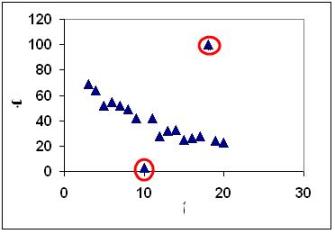
القيم المتطرفة Outliers:
من فوائد هذا الرسم (المخطط) أننا نكتشف القيم المتطرفة بمجرد النظر. ففي كثير من الحالات تجد أن البينات كلها مبعثرة ولكن في منطقة محدودة وهناك قيمة أو أكثر بعيدة كل البعد عن باقي القيم. هذه القيمة أو القيم تسمى نقاط متطرفة أو بيانات متطرفة بمعنى أنها بيانات خارجة عن مجموعة البيانات. هذه القيم المتطرفة قد تكون بسبب:
1- خطأ في تسجيل أو تجميع البيانات
2- وجود حالات نادرة لها أسبابها في البيانات فمثلا عند رسم العلاقة بين الدخل والسن فقد تجد معظم البيانات تقع في مدى محدود وهناك قيم قليلة متطرفة للأثرياء بشكل كبير. فهذه قيم متطرفة ولكنها حقيقية.
3- وجود مجموعتين من البيانات مما يعني الحاجة لدراسة كل منهما على حدة فمثلا عندما تدرس علاقة وقت تصنيع جزء ما بجودة المواد الخام فقد تجد قيما متطرفة إن كان هناك نوعين أو أكثر من المنتجات وفي هذه الحالة سيكون من الأفضل دراسة كلا منهما بشكل منفصل.
القيم المتطرفة تحتاج دراسة لأنها قد تدلنا على وجود مشكلة في تجميع البيانات فنقوم بتصحيحها أو تدلنا على وجود حالات نادرة فنحاول دراسة سببها أو تدلنا على وجود مجموعات مختلفة فنقوم بدراستها. على أي حال فإننا أحيانا قد نهمل القيم المتطرفة إذا كانت قيما خاطئة أو خارجة عن نطاق دراستنا ولكن هذا لا يعني إهمال أي قيم لمجرد عدم رغبتنا في عرضها. ولذلك فمن الأفضل توضيح هذه القيم التي استبعدت وسبب استبعادها.
في المقالات التالية إن شاء الله نستعرض وسائل تحديد قوة العلاقة بين متغيرين وكذلك تحديد معادلة رياضية تصف هذه العلاقة.