تويت
افترض أنك مدير لمؤسسة خدمية وتريد أن تعرف تأثير تقليل زمن الخدمة على طول مدة الانتظار وعلى عدد المنتظرين، أو افترض أنك مدير عملية صناعية وتريد معرفة تأثير حجم المخزون نصف المصنع على زمن تحويل المادة الخام إلى منتج نهائي، كيف تدرس هذه المسألة؟ هناك طرق حسابية عديدة مثل نظرية الطوابير ولكن هناك قانونا بسيطا وعاما يساعدنا كثيرا في مثل هذه الحالات وهذا القانون هو قانون ليتل Little’s Law وهو قانون شهير في الهندسة الصناعية.
ما هو قانون ليتل (لِتل)؟
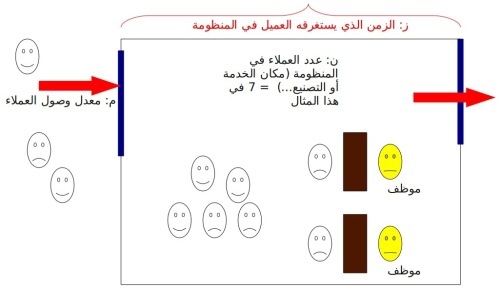
وكلمة Little هنا لا تعني قليل بل هي نسبة لاسم العالم الذي توصل لهذا القانون وهو جون ليتل John Little. ينص قانون ليتل على أن عدد العملاء في المنظومة يساوي حاصل ضرب معدل وصول العملاء X الزمن الذي يستغرقه العميل في المنظومة. افترض أن:
ن: عدد العملاء في المنظومة
م: معدل وصول العملاء
ز: الزمن الذي يستغرقه كل عميل في المنظومة
يمكن أن نكتب قانون ليتل الآن كلآتي:
قانون بسيط ولكنه مفيد جدا ومتعدد التطبيقات. ويتميز هذا القانون بأنه يصلح للتطبيق على أي عملية انتظار بغض النظر عن التوزيع الرياضي لزمن العملية (الخدمة) وبغض النظر عن التوزيع الرياضي لمعدل الحضور وبغض النظر عن عدد مقدمي الخدمة (عدد الماكينات)، وهذا يجعله قانونا واسع التطبيق. والشرط الوحيد لتطبيقه هو أن تكون المنظومة في حالة استقرار أي أن المعدلات ثابتة.
مثال: نحن نقوم بتوزيع بعض المساعدات على المحتاجين وقد تابعنا معدل الحضور خلال ساعة كاملة فوجدناه 30 عميلا أي أن معدل الحضور = 30/60= 0.5 عميل في الدقيقة، وقد وجدنا أن العميل يستغرق اثنا عشر دقيقة في المتوسط بين حضوره وانصرافه، كيف نحسب العدد المتوسط للمتواجدين في مكان تقديم الخدمة؟
نستخدم قانون ليتل ونحن نعلم ان م = 0.5 عميل في الدقيقة، وأن ز= 12 دقيقة
متوسط عدد العملاء داخل مقر الخدمة = 0.5 * 12 = 6 عملاء
معدل وصول العملاء = 60 عميلا في الساعة أي عميل في الدقيقة، والزمن الذي يقضيه العميل هو 45 دقيقة
عدد المقاعد (عدد العملاء في المطعم) = 1 * 45 = 45 مقعدا
مدة الانتظار = م / ن = 200 / 50 = 4 أيام
ماذا لو لاحظنا أن معدل الطلب قد زاد إلى 250 طلبا في اليوم؟ في هذه الحالة علينا أن نخبر العميل أن الزمن المتوقع للانتظار = 250 / 50 = 5 أيام.
فقانون ليتل هنا يساعدنا على توقع مدة الانتظار وبالتالي نستطيع أن نعطي العميل معلومة -ولو تقريبية- لمدة الانتظار المعتادة لمثل هذا الطلب حسب معدل الطلب.
هذا القانون يمكن كتابته بصور أخرى مثل:
مثال: افترض أننا نقدم خدمة ومعدل حضور العملاء لطلب هذه الخدمة هو 3 عملاء في الدقيقة، ولا نريد أن يزيد طول طابور الانتظار عن 6 عملاء، فما هو زمن الخدمة المطلوب؟
زمن الخدمة (ز)= ن / م = 6 / 3 = 2 دقيقة
علينا أن نعمل حتى يكون زمن الخدمة أقل من أو يساوي دقيقتان لكي لا يزيد طول الطابور عن ستة عملاء.
ماذا لو وصل معدل حضور العملاء في ساعة الذروة إلى 12 عميلا في الدقيقة وما زلنا لا نريد أن يزيد طول الطابور عن 6 عملاء؟
علينا أن نقلل زمن الخدمة حتى يساوي = 6 / 12 = 0.5 دقيقة، ولهذا فقد نضطر لزيادة عدد مقدمي الخدمة إلى أربعة أضعاف
مثال: افترض أن معدل إنتاج عملية تصنيعية هو 20 وحدة في الساعة وأن المخزون المتوسط قبل هذه المرحلة هو 60 وحدة، فما هو الزمن المتوسط لتخزين القطعة قبل هذه المرحلة؟المخزون قبل أي عملية تصنيعية = معدل الإنتاج (وحدة/زمن) * زمن التخزين فبل العملية التصنيعية
60 = 20 * زمن التخزين فبل العملية التصنيعية
زمن التخزين قبل هذه العملية = 60 / 20 = 3 دقائق
ماذا لو كان المخزون نصف المصنع قبل هذه المرحلة هو 600 قطعة. في هذه الحالة سيكون زمن التخزين (الانتظار قبل التصنيع) هو 600 / 20 = 30 دقيقة. هذه نتيجة مهمة فهي تبين لنا أن زيادة المخزون نصف المصنع يعني طول مدة الانتظار قبل التشغيل وكلما أطلت هذا الزمن قبل كل مرحلة فإن الزمن الكلي لتحويل المادة الخام لمنتج نهائي يزيد كثيرا، لذلك فإن تقليل المخزون نصف المصنع هو وسيلة لتسريع عملية التصنيع. فعندما يطلب عميلا منتجا فإننا نحاول تلبية طلبه بسرعة وهذا يعني أننا لا نريد للمنتجات نصف المصنعة أن تنتظر فترات طويلة قبل كل مرحلة تصنيع.
وهناك ملاحظة أخرى حول هذا المثال. إن الإنتاجية القصوى لعملية ما هو رقم ثابت للعملية وبالتالي فإن زيادة المخزون نصف المصنع عن ما نحتاجه لتحقيق الإنتاجية القصوى لن يؤدي سوى لزيادة زمن التخزين وكمية المخزون وهو ما لا نريده. فمثلا لو كانت الطاقة الإنتاجية القصوى للماكينة هي 500 قطعة في اليوم فإن تخزين 1000 قطعة قبل تلك الماكينة لن يؤدي لزيادة طاقتها ولكنه يعني طول مدة التخزين وتعاظم كميته يوما بعد آخر.
قانون ليتل هو قانون بسيط ولكنه يساعدنا على ربط مؤشرات الانتظار وحساب مدة الانتظار أو عدد المنتظرين.
ما هو قانون ليتل (لِتل)؟
وكلمة Little هنا لا تعني قليل بل هي نسبة لاسم العالم الذي توصل لهذا القانون وهو جون ليتل John Little. ينص قانون ليتل على أن عدد العملاء في المنظومة يساوي حاصل ضرب معدل وصول العملاء X الزمن الذي يستغرقه العميل في المنظومة. افترض أن:
ن: عدد العملاء في المنظومة
م: معدل وصول العملاء
ز: الزمن الذي يستغرقه كل عميل في المنظومة
يمكن أن نكتب قانون ليتل الآن كلآتي:
ن = م X ز
مثال: نحن نقوم بتوزيع بعض المساعدات على المحتاجين وقد تابعنا معدل الحضور خلال ساعة كاملة فوجدناه 30 عميلا أي أن معدل الحضور = 30/60= 0.5 عميل في الدقيقة، وقد وجدنا أن العميل يستغرق اثنا عشر دقيقة في المتوسط بين حضوره وانصرافه، كيف نحسب العدد المتوسط للمتواجدين في مكان تقديم الخدمة؟
نستخدم قانون ليتل ونحن نعلم ان م = 0.5 عميل في الدقيقة، وأن ز= 12 دقيقة
متوسط عدد العملاء داخل مقر الخدمة = 0.5 * 12 = 6 عملاء
– – – – – – – – – – – –
مثال: افترض أنك تدير مطعما وتتوقع وصول ستين عميلا في ساعة الذروة، وعادة يمضي العميل 45 دقيقة في المطعم، فما عدد المقاعد المطلوبة؟معدل وصول العملاء = 60 عميلا في الساعة أي عميل في الدقيقة، والزمن الذي يقضيه العميل هو 45 دقيقة
عدد المقاعد (عدد العملاء في المطعم) = 1 * 45 = 45 مقعدا
– – – – – – – – – – – –
مثال: نحن مؤسسة تقوم بتلقي طلبات استخراج وثيقة ما عبر الإنترنت ثم ندرس الطلبات ونصدر الوثيقة ونرسلها للعميل. فإذا كان معدل وصول الطلبات هو 50 طلبا في اليوم، وكان عدد الطلبات التي تنتظر الدراسة هي في المتوسط 200 طلبا فما هو الزمن المتوقع قبل تلبية طلب العميل أي ما هي مدة انتظار العميل حتى يصله طلبه؟مدة الانتظار = م / ن = 200 / 50 = 4 أيام
ماذا لو لاحظنا أن معدل الطلب قد زاد إلى 250 طلبا في اليوم؟ في هذه الحالة علينا أن نخبر العميل أن الزمن المتوقع للانتظار = 250 / 50 = 5 أيام.
فقانون ليتل هنا يساعدنا على توقع مدة الانتظار وبالتالي نستطيع أن نعطي العميل معلومة -ولو تقريبية- لمدة الانتظار المعتادة لمثل هذا الطلب حسب معدل الطلب.
– – – – – – – – – – – –
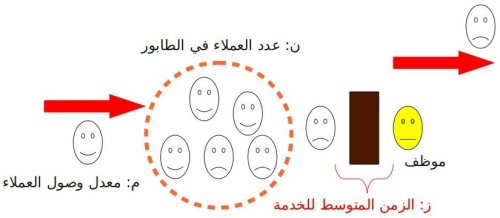
تطبيقات متنوعةهذا القانون يمكن كتابته بصور أخرى مثل:
عدد العملاء في الطابور = معدل وصول العملاء * الزمن المتوسط للخدمة
زمن الخدمة (ز)= ن / م = 6 / 3 = 2 دقيقة
علينا أن نعمل حتى يكون زمن الخدمة أقل من أو يساوي دقيقتان لكي لا يزيد طول الطابور عن ستة عملاء.
ماذا لو وصل معدل حضور العملاء في ساعة الذروة إلى 12 عميلا في الدقيقة وما زلنا لا نريد أن يزيد طول الطابور عن 6 عملاء؟
علينا أن نقلل زمن الخدمة حتى يساوي = 6 / 12 = 0.5 دقيقة، ولهذا فقد نضطر لزيادة عدد مقدمي الخدمة إلى أربعة أضعاف
– – – – – – – – – – – –
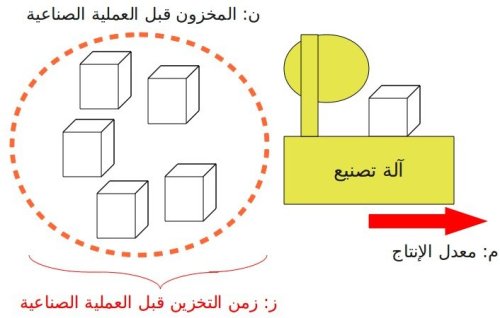
وقد يستخدم قانون ليتل في العمليات الصناعية فيكتب كالتالي:المخزون قبل أي عملية تصنيعية = معدل الإنتاج (وحدة/زمن) * زمن التخزين فبل العملية التصنيعية
60 = 20 * زمن التخزين فبل العملية التصنيعية
زمن التخزين قبل هذه العملية = 60 / 20 = 3 دقائق
ماذا لو كان المخزون نصف المصنع قبل هذه المرحلة هو 600 قطعة. في هذه الحالة سيكون زمن التخزين (الانتظار قبل التصنيع) هو 600 / 20 = 30 دقيقة. هذه نتيجة مهمة فهي تبين لنا أن زيادة المخزون نصف المصنع يعني طول مدة الانتظار قبل التشغيل وكلما أطلت هذا الزمن قبل كل مرحلة فإن الزمن الكلي لتحويل المادة الخام لمنتج نهائي يزيد كثيرا، لذلك فإن تقليل المخزون نصف المصنع هو وسيلة لتسريع عملية التصنيع. فعندما يطلب عميلا منتجا فإننا نحاول تلبية طلبه بسرعة وهذا يعني أننا لا نريد للمنتجات نصف المصنعة أن تنتظر فترات طويلة قبل كل مرحلة تصنيع.
وهناك ملاحظة أخرى حول هذا المثال. إن الإنتاجية القصوى لعملية ما هو رقم ثابت للعملية وبالتالي فإن زيادة المخزون نصف المصنع عن ما نحتاجه لتحقيق الإنتاجية القصوى لن يؤدي سوى لزيادة زمن التخزين وكمية المخزون وهو ما لا نريده. فمثلا لو كانت الطاقة الإنتاجية القصوى للماكينة هي 500 قطعة في اليوم فإن تخزين 1000 قطعة قبل تلك الماكينة لن يؤدي لزيادة طاقتها ولكنه يعني طول مدة التخزين وتعاظم كميته يوما بعد آخر.
قانون ليتل هو قانون بسيط ولكنه يساعدنا على ربط مؤشرات الانتظار وحساب مدة الانتظار أو عدد المنتظرين.
تعليق